37. 解数独 [hard]

https://leetcode-cn.com/problems/sudoku-solver/

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 '.' 表示。

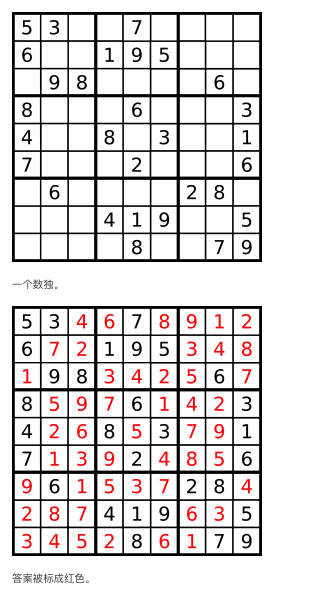
Note:

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

通过次数30,755 | 提交次数49,782

First Try

确实挺有难度的，由于已经有36题的经验，处理小矩阵没什么问题，但是第一遍依然是没有什么思路，就算用暴力法也有点无从下手。初步是使用set的交集获取每个位置的所有可能，然后遍历所有可能，但如何在所有可能中进行遍历并更新还是无从下手。感觉应该构造一个递归的形式，但在遍历所有位置的操作中也不知道怎么写出一个递归。

偷窥了题解获取到基本思路：回溯法+约束编程。知道使用回溯法，还是头疼了许久如何确定循环和回溯。慢慢才确定了循环的模式，在成功的时候如何进行跳出，在失败的时候如何进行状态恢复，并且继续遍历。还是花了挺长时间的，几个小时都有了，又是一道无法在规定时间内完成的题目。

虽然仍然因为耗时太久而倦怠失落，不过做完之后，还是有一些成就感。

class Solution(object):
    def solveSudoku(self, board):
        """
        :type board: List[List[str]]
        :rtype: None Do not return anything, modify board in-place instead.
        """
        n = len(board)
        gen_set = lambda: set([str(i) for i in range(1, 10)])
        rows = [gen_set() for i in range(n)]
        columns = [gen_set() for i in range(n)]
        matrix = [gen_set() for i in range(n)]
        matrix_idx = lambda i, j: i // 3 * 3 + j // 3

        for i in range(9):
            for j in range(9):
                t= board[i][j]
                if t == ".":
                    continue
                rows[i].remove(t)
                columns[j].remove(t)
                matrix[matrix_idx(i,j)].remove(t)
                
        available_slots = lambda i, j: rows[i].intersection(columns[j]).intersection(matrix[matrix_idx(i, j)])
        jump_next_idx = lambda i, j: (i + 1, 0) if j == n - 1 else (i, j + 1)
        def backtrack(i, j):
            if (i, j) == (n, 0): # success point
                return True
            # print(i, j, board[i][j], available_slots(i, j))
            if board[i][j] != ".":
                return backtrack(*jump_next_idx(i, j))  # to be determined by next point
            if not available_slots(i, j):
                return False
            for num in available_slots(i, j):
                # print("wtf", num, available_slots(i, j), i, j)
                board[i][j] = num
                rows[i].remove(num)
                columns[j].remove(num)
                matrix[matrix_idx(i,j)].remove(num)
                r = backtrack(*jump_next_idx(i, j))  # next item
                if r:
                    return True
                board[i][j] = "."
                rows[i].add(num)
                columns[j].add(num)
                matrix[matrix_idx(i, j)].add(num)
            return False
        backtrack(0, 0)

执行用时 :128 ms, 在所有 Python 提交中击败了65.80%的用户
内存消耗 :13.1 MB, 在所有 Python 提交中击败了100.00%的用户

37. 解数独 [hard]​

First Try​

37. 解数独 [hard]

First Try