688. “马”在棋盘上的概率[medium]

https://leetcode-cn.com/problems/knight-probability-in-chessboard

已知一个 NxN 的国际象棋棋盘，棋盘的行号和列号都是从 0 开始。即最左上角的格子记为 (0, 0)，最右下角的记为 (N-1, N-1)。

现有一个 “马”（也译作 “骑士”）位于 (r, c) ，并打算进行 K 次移动。

如下图所示，国际象棋的 “马” 每一步先沿水平或垂直方向移动 2 个格子，然后向与之相垂直的方向再移动 1 个格子，共有 8 个可选的位置。

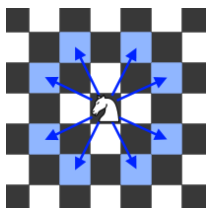
现在 “马” 每一步都从可选的位置（包括棋盘外部的）中独立随机地选择一个进行移动，直到移动了 K 次或跳到了棋盘外面。

求移动结束后，“马” 仍留在棋盘上的概率。

示例：

输入: 3, 2, 0, 0
输出: 0.0625
解释: 
输入的数据依次为 N, K, r, c
第 1 步时，有且只有 2 种走法令 “马” 可以留在棋盘上（跳到（1,2）或（2,1））。对于以上的两种情况，各自在第2步均有且只有2种走法令 “马” 仍然留在棋盘上。
所以 “马” 在结束后仍在棋盘上的概率为 0.0625。

注意：

N 的取值范围为 [1, 25]
K 的取值范围为 [0, 100]
开始时，“马” 总是位于棋盘上

通过次数3,422 | 提交次数7,265

First Try

2020-06-13

换个思路，在每一轮的时候落在某个位置的概率为prob[i][j], 下一轮的时候按照概率进行叠加计算。走了k轮之后，落在所有位置都有特定的概率，加起来即可。问题甚至可以升级为，走了k轮之后，落在i，j位置的概率为多少。这种全棋盘保存状态的思路也是很有意思，怎么我又没在第一时间想到，f**k。

复杂度变成了 O(N N K * 8),虽然仍然是多项式，但比起之前的指数爆炸，已经好太多了。

class Solution(object):
    def knightProbability(self, N, K, r, c):
        """
        :type N: int
        :type K: int
        :type r: int
        :type c: int
        :rtype: float

        换个思路，在每一轮的时候落在某个位置的概率为prob[i][j], 下一轮的时候按照概率进行叠加计算
        走了k轮之后，所有位置都有概率，加起来即可。
        问题甚至可以升级为，走了k轮之后，落在i，j位置的概率为多少
        这种全棋盘保存状态的思路也是很有意思，怎么我又没想到，f**k
        """

        steps = [(-2, -1), (-2, 1), (-1, -2), (-1, 2), (1, -2), (1, 2), (2, -1), (2, 1)]
        # 这个写法还是有bug
        prev_prob = [[0 for j in range(N)] for i in range(N)] 
        prev_prob[r][c] = 1
        for _ in range(0, K):
            # 每一轮都重新开始，避免受影响。其实每次都开创新空间，不过还好每次也都扔掉旧空间，算起来空间使用量还是比较低。
            next_prob = [[0 for j in range(N)] for i in range(N)]
            for i in range(N):
                for j in range(N):
                    for p, q in steps:
                        if(0 <= i + p <= N-1 and 0<= j + q <= N-1):
                            next_prob[i+p][j+q] +=  prev_prob[i][j] * 1.0/8
            prev_prob = next_prob
        rv =  sum([sum(prev_prob[i]) for i in range(N)])
        return rv

执行用时 :236 ms, 在所有 Python 提交中击败了.48%的用户
内存消耗 :12.6 MB, 在所有 Python 提交中击败了100.00%的用户

Bug Try

棋盘位置写法(failed)

每一轮的概率取决于前一轮的情况，如果每次只影响i,j之前的位置，则只用一个NN矩阵即可，但马可往前往后跳，容易出现在一轮中重复计算的问题，因此至少使用两个矩阵，或者使用NN*K矩阵保存第K次位置的概率。

为了压缩使用了两个矩阵（prev, next)，但是bug仍然存在。如果每一轮不对next进行清空的话，计算[i][j]位置概率叠加的时候直接把上一轮在[i][j]位置的概率也加进来了，问题是上一轮在[i][j]位置的棋子，下一轮不可能继续在[i][j]，悲剧就发生了。

换个思路
class Solution(object):
    def knightProbability(self, N, K, r, c):
        """
        :type N: int
        :type K: int
        :type r: int
        :type c: int
        :rtype: float

        换个思路，在每一轮的时候落在某个位置的概率为prob[i][j], 下一轮的时候按照概率进行叠加计算
        走了k轮之后，所有位置都有概率，加起来即可。
        问题甚至可以升级为，走了k轮之后，落在i，j位置的概率为多少
        这种全棋盘保存状态的思路也是很有意思，怎么我又没想到，f**k
        """

        steps = [(-2, -1), (-2, 1), (-1, -2), (-1, 2), (1, -2), (1, 2), (2, -1), (2, 1)]

        # 这个写法还是有bug
        # 每一轮的概率取决于前一轮的情况，如果只用一个矩阵，会导致重复计算的问题。
        # 如果每次只影响i,j之前的位置，则只用一个矩阵即可，但马可往前跳，导致容易出现在一轮中重复计算的问题
        prob = [[[0 for j in range(N)] for i in range(N)] for k in range(2)] 
        prob[0][r][c] = 1
        for k in range(1, K + 1):
            for i in range(N):
                for j in range(N):
                    for p, q in steps:
                        if(0 <= i + p <= N-1 and 0<= j + q <= N-1):
                            prob[k % 2][i+p][j+q] +=  prob[(k-1)%2][i][j] * 1.0/8
        rv =  sum([sum([prob[K % 2][i][j]for j in range(N)]) for i in range(N)])
        return rv

指数爆炸写法(failed)

首先缓存一波所有位置在走一步后仍然停留在棋盘的概率，然后对下一步的每个位置进行遍历叠加。每一步的下一步有8个可能，属于8 ^ k次方，直接就爆炸了。

class Solution(object):
    def knightProbability(self, N, K, r, c):
        """
        :type N: int
        :type K: int
        :type r: int
        :type c: int
        :rtype: float

        首先缓存一波所有位置在走一步后仍然停留在棋盘的概率，然后每一步进行遍历
        但是这样以来，每一步的下一步有8个可能，属于8 ^ k次方，这tmd是要爆炸啊

        prob[i][j] = inside_boundary([i+-2][j+-1], [i+-1][j+-1])
        prob[r][c] -> prob[r][c] * (prob[i][j] of next 8 possible position) * ( 8 ^ 2)

        """
        prob = [[0 for i in range(N)] for j in range(N)]
        steps = [(-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (-1, -2), (-2, -1)]
        for i in range(N):
            for j in range(N):
                if(2 <= j <= N - 3 and 2 <= i <= N - 3):
                    prob[i][j] = 1
                    continue
                for p, q in steps:
                    if(0 <= i + p <= N - 1 and 0 <= j + q <= N - 1):
                        prob[i][j] += 1.0 / 8 
        for i in range(K):
            prob[r][c] *  # 写不动了不对