1489. 找到最小生成树里的关键边和伪关键边 [hard]
1489. 找到最小生成树里的关键边和伪关键边 [hard]
https://leetcode-cn.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/
给你一个 n 个点的带权无向连通图,节点编号为 0 到 n-1 ,同时还有一个数组 edges ,其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集,它连接了所有节点且没有环,而且这些边的权值和最小。
请你找到给定图中最小生成树的所有关键边和伪关键边。如果从图中删去某条边,会导致最小生成树的权值和增加,那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。
请注意,你可以分别以任意顺序返回关键边的下标和伪关键边的下标。
示例 1:
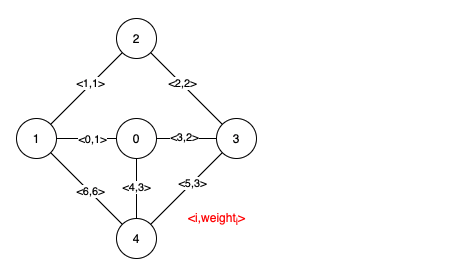
输入:n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
输出:[[0,1],[2,3,4,5]]
解释:上图描述了给定图。 下图是所有的最小生成树。
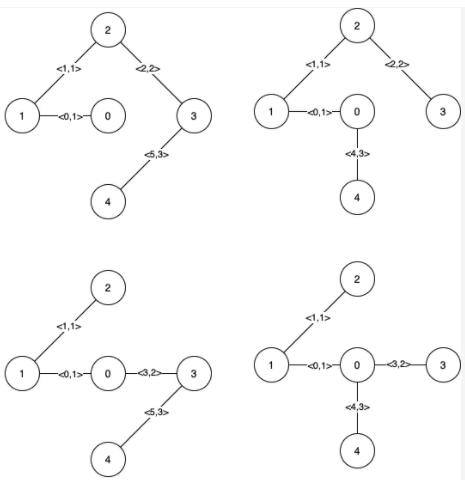
注意到第 0 条边和第 1 条边出现在了所有最小生成树中,所以它们是关键边,我们将这两个下标作为输出的第一个列表。 边 2,3,4 和 5 是所有 MST 的剩余边,所以它们是伪关键边。我们将它们作为输出的第二个列表。
示例 2 :
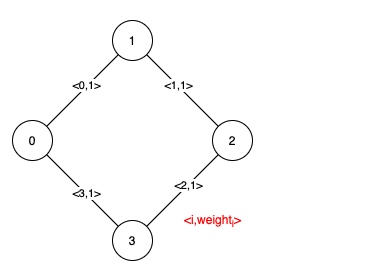
输入:n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
输出:[[],[0,1,2,3]]
解释:可以观察到 4 条边都有相同的权值,任选它们中的 3 条可以形成一棵 MST 。所以 4 条边都是伪关键边。
提示:
- 2 <= n <= 100
- 1 <= edges.length <= min(200, n * (n - 1) / 2)
- edges[i].length == 3
- 0 <= fromi < toi < n
- 1 <= weighti <= 1000
- 所有 (fromi, toi) 数对都是互不相同的。
通过次数564 | 提交次数1,241
Second Try
2020-07-02
prim算法来一波
prim算法是从点的角度来考虑问题的,其实并不是最适合这道题的解法,更适合的是kruskal算法。
最小生成树的核心重点是分割集和树的概念。对于一个图中的包含所有顶点的树,其特点一是所有顶点都被包含;其次是任意连接两个定点,如果不属于树的边,则会构成一个图;三是任意断开树的一条边,都会变成两棵树。这些特点构成来分割集的基础。假设目前有一个最小生成树,其总长度是tot,断开其中的一条边x, 则变成了两个分割集。在分割集中有n条边可以把这两个分割集合并起来,其中只有最小权重的边x才是属于最小生成树的边。继续用反证法,如果不是x而是任意一条其他边y,则在形成树之后,总长度是tot - x + y。这时候把x继续连接上去,形成了一个环,这个环中必然包括y边(这个是关键)。 把环上的y去掉,则又成了一棵树,这棵树长度为tot。由于x < y, 则tot < tot - x + y. 因此在两个分割集中的最小边,就是最小生成树的一部分。
以此类推,prim算法的想法是从一个点的集合和其他所有点构成的集合来考虑,环绕这个起点的所有边的最小权重边就是最小生成树的第一条边。然后沿着这条边的两个定点不断扩散,将这两个定点连接的所有边都放到优先队列里去排序,以此拿出最小边,只要这个最小边不会导致已有的树形成一个环,则该边有效。
该证明挺有意思的,总担心不严谨但其实这就是官方证明。。。
而kruskal算法也是类似,但是是从边的角度来考虑。不像prim算法随意的制定一个点开始扩散,kurskal算法一开始就是从最小边开始的,第一条最小边也间接选定了开始点。从边的角度来考虑,只要这条边的两个点属于两个不同的集合, 反而更有分割集的基本含义的概念。因此kruskal算法的另一个核心是判断一条最小边的两个点是否在两个不同集合内,如果在同一个集合内则说明会形成环,也说明有更小的边在之前已经被选择过了,直接跳过即可。
因此prim算法的实现上,需要使用优先队列,而在考察某条边是否有效的时候,直接判断是否两个定点都被访问过即可,因为从1开始扩散最多只会有1棵树。
而kurskal算法则在一开始可能有n棵不同的小树,慢慢扩散才会融合为1棵最小生成树。kruskal算法需要使用union find来判断一条边的两个点是否已经在同一个集合内,但是并不需要使用优先队列对边进行动态更新,只需要在一开始排好序就可以了。
针对这个题目,没想到其实使用暴力遍历法来解决的。对于关键边的定义,其实就是去除这条边之后,是否还有最小生成树,或者最小生成树的高度是否比之前高,那么说明这确实是不可丢失的关键边。对于伪关键边,则可以考虑如果一开始就强行要求加入这条边,是否会导致最小生成树的高度变化,没变化则说明确实存在于某棵最小生成树内。因此在前面的prim和kruskal算法里加上这两个对边的筛选操作就可以完成任务。
bingo,又是一道花费几个小时学会的经典算法题,虽然algs4看过,但还是比不上按需解决写代码,而且还有完善的测试案例。。。
# prim 来一波
import heapq
class Solution(object):
def findCriticalAndPseudoCriticalEdges(self, n, edges):
"""
:type n: int
:type edges: List[List[int]]
:rtype
"""
graph = collections.defaultdict(list)
nedges = []
for i, (f, t, w) in enumerate(edges):
ne = (w, f, t, i)
graph[f].append(ne)
graph[t].append(ne)
nedges.append(ne)
print(nedges)
def prim(selected, insert, remove):
heap = []
# prim因为总是只有1颗树,因此用visited数组即可,不想kruskal需要用union find
# 而且kruskal需要判断是否形成环,也需要union find. 不过kruskal可以也用visted吗?
visted = [0 for i in range(n)]
mst = []
weight = 0
start_point = [0]
# 保证某条边被包括进去,提前把两个节点固定好,琐碎的关联参数不能遗漏
if insert:
w, f, t, i = selected
visted[f] = visted[t] = True
mst.append(selected)
weight += w
# 如果仍然从0开始,会导致出现两棵树
# 而且每个加入的点的连接边都得加进去,如果只任意选择一个点,会导致另一个点的其他边都被排斥掉
# start_point = f
start_point = [f, t]
# 总归每次从节点0开始
# for edge in graph[0]:
# heapq.heappush(heap, edge)
# visted[0] = 1
for sp in start_point:
visted[sp] = 1
for edge in graph[sp]:
heapq.heappush(heap, edge)
# 每次从所有与当前树有关系的边中选出最短的一条,看能否作为最短横切边
while(len(heap)):
edge = heapq.heappop(heap)
w, f, t, i = edge
# 剔除某条边
if remove and selected == edge:
# print('vola')
continue
if visted[f] and visted[t]:
# print("wtf")
continue
visted[f] = visted[t] = 1
weight += w
mst.append(edge)
for edge in graph[f]:
heapq.heappush(heap, edge)
for edge in graph[t]:
heapq.heappush(heap, edge)
if len(mst) == n - 1:
break
# print(insert, remove, mst, weight)
if len(mst) != n-1:
return float('inf')
return weight
minw = prim(None, False, False)
# print("min", minw)
rv = [[],[]]
for edge in nedges:
# print("******", edge[-1])
remw = prim(edge, insert=False, remove=True)
# print("remove", edge[1], edge[2], edge, remw)
if remw > minw:
rv[0].append(edge[-1])
else:
insertw = prim(edge, insert=True, remove=False)
# print('insert', edge[1], edge[2], edge, insertw)
if insertw == minw:
rv[1].append(edge[-1])
return rv
First Try
2020-07-01
终于来了一波kruskal算法,虽然对于证明部分还有点迷糊,至少实践了一波。而题解其他部分是看着题解一路坐下来的,根本想不到还能用暴力遍历法。
另外发现如果在运行中print内容,会导致额外多出许多时间,本次把debug过程中的print删掉,提交竟然从3.8s变成1.8s。
kurskal算法和prim算法的详情看second try里的小结。在algs4里看完prim,就看不下去kurskal了,还是得上手写一波才行,工程师思维模式。
import heapq
class Solution(object):
def findCriticalAndPseudoCriticalEdges(self, n, edges):
"""
:type n: int
:type edges: List[List[int]]
:rtype: List[List[int]]
"""
# 终于可以练手来一波最小生成树
# 虽然看过书,但没精力的时候对证明已经很难看下去来
# heap = []
# for f, t, w in edges:
# heapq.heappush(heap, [w, f, t])
edges = sorted([[w, f, t, i] for i, (f, t, w ) in enumerate(edges)])
def find_root(graph, node):
if graph[node] != node: # 写成while直接掉入无限循环
graph[node] = find_root(graph, graph[node])
# print('root', node, graph[node])
return graph[node]
def union(graph, ni, nii):
if ni == nii:
return False
root_i = find_root(graph, ni)
root_ii = find_root(graph, nii)
if root_i == root_ii:
return False
graph[root_i] = root_ii
return True
def kruskal(check_edge, insert, skip):
graph = [i for i in range(n)]
mst = []
mstlen = 0
# 强行加入树中,只要合并两个点就被认为加入树中了
if insert:
union(graph, check_edge[1], check_edge[2])
mstlen += check_edge[0]
mst.append(check_edge) # f**k,忘记加了导致一直出错。。
# print("insert", check_edge)
for edge in edges:
w, f, t, i = edge
if skip and f == check_edge[1] and t == check_edge[2]:
continue
if union(graph, f, t):
mst.append([w, f, t, i])
mstlen += w
if len(mst) == n - 1:
break
# print(mst)
if len(mst) != n-1:
return float('inf')
return mstlen
rv = [[], []]
minw = kruskal(None, False, False)
# print("min len", minw)
for edge in edges:
slen = kruskal(edge, insert=False, skip=True)
if slen == float('inf') or slen > minw:
rv[0].append(edge[-1])
else:
ilen = kruskal(edge, insert=True, skip=False)
# print(ilen)
if ilen == minw:
rv[1].append(edge[-1])
return rv
- 执行用时:1388 ms, 在所有 Python 提交中击败了75.00%的用户
- 内存消耗:12.7 MB, 在所有 Python 提交中击败了100.00%的用户