1547. 切棍子的最小成本 [hard]

https://leetcode-cn.com/problems/minimum-cost-to-cut-a-stick/

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的最小总成本。

示例 1：

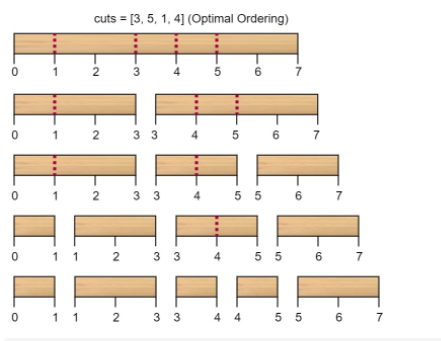
输入：n = 7, cuts = [1,3,4,5]
输出：16

解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

)

第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4，6，5，2，1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
cuts 数组中的所有整数都互不相同

通过次数2,260 | 提交次数4,511

First Try

2020-09-02

朴素的解法以为每次寻找离中间最近的点进行切割就是最优解，但是在某个测试案例上失败了。

看官方题解才知道是一道朴素的动态规划的题目，底层其实是暴力遍历法，没想到竟然能够通过。

虽然n是10^6级别，但是cuts其实最大只有100，这为暴力法奠定了基础。

复杂度计算粗看有点无法下手，参考官方题解的分析方法: m为所有cuts的数量，总共的状态有m * m个，每个状态需要遍历所有m个切割的可能，因此复杂度为O(m^3).

把0和n添加到cuts，这样所有的断点选择就在cuts里面了，无需考虑本身n的大小。

状态方程dp[i][j]代表左右端点为cuts[i]和cuts[j]的棍子的最小切割长度，在计算的时候需要遍历下一个切割在i和j之间的所有可能找到最小值，然后递归法就解决了。

看评论这个动态规划的通用叫法叫做区间动态规划。

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        cuts.extend([0, n])  # 把首尾放进来，只需要考虑cuts
        cuts = sorted(cuts)
        len_cuts = len(cuts)
        cache = [[''] * (len_cuts + 1) for _ in range(len_cuts + 1)]
        
        def min_cut(start, end):
            if cache[start][end] != "":
                return cache[start][end]
            if end - start == 1: #中间没有cuts了
                return 0 
            minv = float('inf') 
            for cidx in range(start + 1, end):
                minv = min(minv, min_cut(start, cidx) + min_cut(cidx, end))
            cache[start][end] = cuts[end] - cuts[start] + minv
            return cache[start][end]

        rv = min_cut(0, len_cuts - 1)
        return rv   

执行用时：1496 ms, 在所有 Python3 提交中击败了35.08%的用户
内存消耗：15 MB, 在所有 Python3 提交中击败了49.27%的用户

Failed Try

2020-09-02

错误解法，朴素的以为每次从离中间点最近的地方切割就能得到最优解。

两个题目的样例都成功通过了，一提交遇到复杂的例子就挂掉了。

不过没有简单直观的例子，还是不知道在哪种情况下这种思路不对，以至于只能用暴力打表法。

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        # 每次对半切，离中心位置最近的作为切割点可以么？
        cuts = sorted(cuts)  # 不排序可能会出现负值
        def cut(start, end, cuts):
            if start == end or len(cuts) == 0:
                return 0
            mid = (start + end) / 2.0 
            min_idx, min_gap = 0, float('inf')
            for idx, cidx in enumerate(cuts):
                if abs(cidx - mid) < min_gap:
                    min_idx, min_gap = idx, abs(cidx - mid)
            print("start end", start, end, "select cut", cuts[min_idx], end-start)
            rv = (end - start)
            rv += cut(start, cuts[min_idx], cuts[:min_idx])
            rv += cut(cuts[min_idx], end, cuts[min_idx + 1:])
            return rv 

        rv = cut(0, n, cuts)
        return rv 