743. 网络延迟时间 [medium]

https://leetcode-cn.com/problems/network-delay-time/

有 N 个网络节点，标记为 1 到 N。

给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。

现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。

示例：

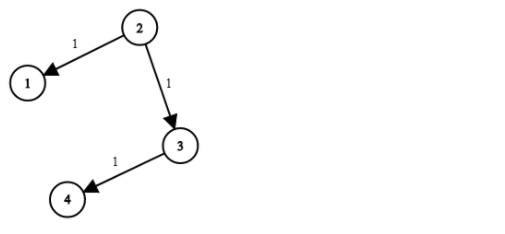
输入：times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出：2

注意:

N 的范围在 [1, 100] 之间。
K 的范围在 [1, N] 之间。
times 的长度在 [1, 6000] 之间。
所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 0 <= w <= 100。

通过次数12,944 | 提交次数28,766

Third Try

2020-06-30

其实回过头来看，自己摸索的first try其实已经是正宗的优化后的dijkstra算法，而我在看题解这个未优化后的算法的时候还懵逼了一会儿。 first try里的思路真是理所当然，拆分成这个原始版本真是突然有点难理解。

每次查找到起点最近距离的一个点，这个点就算被标记了，不用再进循环了。然后这个点下游的所有点，都可以获得一个新的距离，跟本身已经有的距离进行比较，选择小的就完事了，然后开始下一波。在下一波循环中，依然是选择当前到起点最近的一个点，然后继续重复这个过程。反正每次操作，都能够确认一个最短距离点，虽然不一定是同一条路线上的，但每次都会有一个点被解决掉。最后一波N次循环之后，所有点离起点的最短距离也就出来了。最后的时候，判断是否所有点都有有效距离，可以看出是否有些点无法到达没有被遍历到。

每次循环的时候，选择最小点需要N次比较，因此总的算法复杂度是O(N^2),勉强可以接受。

算是真正在实现上搞定了传说多年的dijkstra算法，今天浪费那么多时间也算是值得了。这个领域不再那么玄乎了。不过看算法书上的证明，还是没法硬着头皮看完，看来还是leetcode厉害，至少有个案例可以上手掌握。

又思考了一会儿，其实dijkstra算法的核心在于每轮一开始得到的距离最短的节点，这个节点到起点的距离是所有可能中最短的，因为其他点的距离都要大于该点（其他更短的节点早就被遍历过了，且其所有能到达的下一个节点也都进入此轮比较范围），通过其他点再绕过来的话更不用说。因此这一轮其实真正能确认的是这个距离最短的节点，而这个节点下游的节点的距离仅仅只是做一个初步标记而已，无关紧要。

时间复杂度： EE 是 times 的长度。基础实现方式为 O(N^2 + E)O(N 2 +E)。堆实现方式为 O(E \log E)O(ElogE)，因为每个边都可能添加到堆中。
空间复杂度：O(N + E)O(N+E)，图的大小是 O(E)O(E) 加上其他对象的大小 O(N)O(N)。

2020-07-12 补充记录

做了几天其他题目，再遇到最短路径的时候又开始有些犯迷糊，dijkstra、prim、kruskal都混淆在一起。其实dijkstra算法在每一轮优先队列加入元素的时候，都需要与上一个的结果进行叠加（比如这里的时间相加，比如算概率的时候与上一个概率相乘），而prim算法每一轮只需要离当前树最短的距离的边即可，要简单许多。一个dijkstra算法不做最终限制，得到的是到所有顶点的最短距离，如果到某个顶点就挺住了，则是到某个顶点的最短距离。而prim算法是所有边的总和最短，并不是完全形态的dijkstra算法（到所有顶点的最短路径），虽然不假思索会认为就是同一个。比如很简单的一个案例，考虑一个三角形构成的图，有a,b,c三个点，a为起点，ac边>bc边, 那么dijkstra最短距离分别为a-b和ac两条边。但是最短生成树肯定是a-b和b-c两条边。

如果要知道dijkstra得到最短距离后的路径，那么需要在每次放到队列里的时候，自动把前一个路线的信息合并到该点末尾即可,比如本来是[distance1, node1],下一个关联点是[distance11, node11], 可以改成[distance1 + distance 11, node11, node1]，放进优先队列里，看下一个出来的是哪个。因此每一轮的时候，dijkstra处理的都是里起点距离最近的点。

至于prim最小生成树，要知道所有的边，那么只需要每次添加新点的时候，把边放到集合里即可。毕竟所有点都会被包含，因此统计点只用来判断是否所有点可联通。每一轮循环的时候，prim算法从优先队列里拿到的，都是离当前集合树最近的点，并不是离起点最近的点。

这个差别就差点忘了，还是得总结一下。

# 得来一波真正的dijkstra
class Solution(object):
    def networkDelayTime(self, times, N, K):
        """
        :type times: List[List[int]]
        :type N: int
        :type K: int
        :rtype: int
        """

        graph = collections.defaultdict(list)
        for source, target, time in times:
            graph[source].append([time, target])
        dist = [float('inf') for i in range(0, N+1)]
        dist[K] = 0
        dist[0] = 0 # 填个坑
        visited = set([0])
        while True:
            shortest_p = None
            shortest_dist = float('inf')
            for i in range(1, N+1):  # 写成range(1, N)，又浪费一次提交
                if i not in visited and dist[i] < shortest_dist:
                    shortest_dist = dist[i]
                    shortest_p = i
            # print(shortest_p, graph[shortest_p])
            if shortest_p is None:
                break
            visited.add(shortest_p)
            for t, n in graph[shortest_p]:
                # print(shortest_p, shortest_dist, dist[n], t)
                dist[n] = min(dist[n], shortest_dist + t)
        # print("ala", dist)
        if max(dist) == float('inf'):
            return -1
        return max(dist)

执行用时：576 ms, 在所有 Python 提交中击败了42.20%的用户
内存消耗：14.7 MB, 在所有 Python 提交中击败了100.00%

Second Try

2020-06-20

一个无关紧要的暴力递归版本，从题解了解到dijkstra之后想要写一波，以为有个递归，一写就搞出来这个版本。其实每个定点下面的每个边都被遍历了一遍，甚至如果选择恶化的条件下每个定点的下游会被遍历N遍，因此复杂度是O(N^N)级别，太可怕了。不过在时间测试上竟然也能通过。

时间复杂度：O(N^N + E \log E)O(N N +ElogE)。其中 EE 是 times 的长度。
空间复杂度：O(N + E)O(N+E)，图的大小是 O(E)O(E) 加上 DFS 中隐式调用堆栈的大小 O(N)O(N)。

# 来一波dijkstra（虚假的
class Solution(object):
    def networkDelayTime(self, times, N, K):
        """
        :type times: List[List[int]]
        :type N: int
        :type K: int
        :rtype: int
        """
        graph = collections.defaultdict(list)
        for source, target, time in times:
            graph[source].append([time, target])

        dist = [float("inf") for i in range(0, N+1)] #差点又写成了range(1, N+1)
        dist[K] = 0 
        dist[0] = 0 # 这个无关紧要，占个位置别影响判断
        
        # 所有位置遍历一遍，感觉是一个很蠢的算法，复杂度应该是所有边吧？ 
        # 好像还不止，如果一开始是比较长碰上了，会把下游也都遍历一遍，之后遇到短的又重来一遍，感觉是接近O(N^N)的算法...
        def recursive(node, dist):
            for t, n in graph[node]:
                if dist[node] + t <  dist[n]:
                    dist[n] = dist[node] + t
                    recursive(n, dist)
        recursive(K, dist)
        time = max(dist)
        return -1 if time == float('inf') else time

执行用时：3220 ms, 在所有 Python 提交中击败了5.68%的用户
内存消耗：16.6 MB, 在所有 Python 提交中击败了100.00%的用户

First Try

2020-06-30

其实这个就是早上十几分钟写出来的一个版本，当然是在修改了bug之后的，当时也不知道dijkstra算法之类，就按照题意进行直白翻译了，结果竟然写出了传说中的dijkstra算法。说起来也是出题人牛逼，刚好除了道这么好理解的题目，按照时间排序非常直接自然。而且为了每次获得最近可以到达的顶点，直接使用了优先队列，现在用起来也是很自然了。

复杂度是O(NlgN)吧。

import heapq

class Solution(object):
    def networkDelayTime(self, times, N, K):
        """
        :type times: List[List[int]]
        :type N: int
        :type K: int
        :rtype: int
        """
        # 查找k点到所有节点的最短路径，典型的dijkstra算法
        # 但这里用的是自己摸索的写法，虽然中间出过bug
        graph = collections.defaultdict(list)
        indegree = [i for i in range(N+1)]
        for source, target, time in times:
            graph[source].append([time, target])
            indegree[target] += 1
        # 提前检查一波是否有一些明确不可到达的根节点，但只是加速不检查也不影响结果
        for idx in range(1, N+1):
            if indegree[idx] == 0 and idx != K:
                return -1
        heap = [[0, K]]
        visited = set()  # 严格按照时间排序，后来的就算了
        while len(heap):
            time, node = heapq.heappop(heap)
            if node in visited:  # 虽然加入前检查过，但也可能被插队了
                continue
            # if len(visited) == N:  # 提前跳出看能否加速，然后并没有加速
            #     break
            visited.add(node)
            final_time = time # 最后一次才有效
            for t, n in graph[node]:
                if n in visited:  # 加入前也检查一波是否已经走过了,走过的肯定更早
                    continue
                heapq.heappush(heap, [time + t, n])
        # 其实最后一个从heap出来后没被访问过的元素，就是最后被到达的节点，
        if len(visited) != N:
            return -1
        return final_time
        

执行用时：496 ms, 在所有 Python 提交中击败了60.28%的用户
内存消耗：15.1 MB, 在所有 Python 提交中击败了100.00%的用户

bug version

在队列里排队的元素，没有想到需要用总时间，导致出现低级bug。本来没有这个bug的话，真是是十几分钟就搞完了，结果叠加今天各种琐事摸鱼现在一直到了傍晚了。

# 在队列里排队的元素，没有想到需要用总时间，导致出现低级bug
import heapq
import collections

class Solution(object):
    def networkDelayTime(self, times, N, K):
        """
        :type times: List[List[int]]
        :type N: int
        :type K: int
        :rtype: int
        """
        # 感觉应该使用优先队列
        # 这里的有向图并没有先决条件之类的制约
        # 有向图里面可能有环，一个节点有不同达到路径，可能存在快速捷径
        heap = []
        graph = collections.defaultdict(list)
        # 又傻逼了，为了存储1到N的元素，同时允许直接用元素下表索引，竟然写出了range(1, N+1)这种低级bug
        # indegree = [0 for i in range(1, N+1)]
        indegree = [0 for i in range(0, N+1)]
        for source, target, time in times:
            graph[source].append([time, target])
            indegree[target] += 1
        # 筛选不可能到达的点
        starts = []
        for idx in range(1, N+1):
            if indegree[idx] == 0:
                starts.append(idx)
        # 本身K也不一定是根节点，只是查找下是否有其他根节点
        if len(starts) >= 1 and starts != [K]:
            print("vola", starts, K)
            return -1
        
        # seq = []  # 发现还是得把一路走过的路都记录下; 好像不需要记录所有走过的路，直接放弃
        visited = set()
        # 起始点为[0, K],毕竟顶点不需要时间
        heapq.heappush(heap, [0, K])
        while len(heap):
            item = heapq.heappop(heap)
            time, node = item[0], item[1]
            # 可能被捷足先登了，就算放进去队列的时候已经检查过一次
            if node in visited:  
                continue
            seq_final = item + [] # 最后到达的就是最长的
            visited.add(node)
            for t, n in graph[node]:
                # print(node, n, t)
                if n not in visited:
                    # 前面走过的路都算数
                    heapq.heappush(heap, [t, n] + item)
        if len(visited) != N:
            print("ala?", visited)
            return -1
        print(seq_final)
        total = 0
        for i in range(len(seq_final)):
            if i % 2 == 0:
                total += seq_final[i]
        return total