51. N皇后 [hard]

https://leetcode-cn.com/problems/n-queens/

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

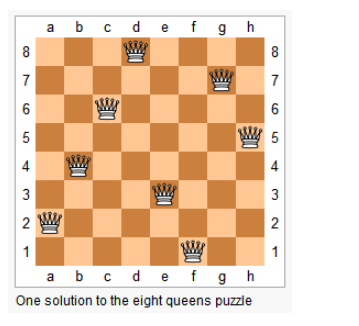
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

解释: 4 皇后问题存在两个不同的解法。

提示：

皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一到七步，可进可退。（引用自百度百科 - 皇后）

note: 提示错误，其实是横竖和斜线延伸都可以吃掉棋子，而不是只有7步的限制。

通过次数51,825 | 提交次数73,597

Second Try

2020-07-28

参考官方题解，对交叉曲线的计算进行优化，速度直接就飙到前5%了。

对角线其实是两根交叉的直线，斜率分别为1和-1，这样i,j坐标的两根斜线特性为i + j为常数和i - j为常数，不在两条线上的点则有不同的常数。判断的时候通过两个集合进行统计，backtrack的时候取消即可，毕竟出现过一次不会再重复。直接把复杂度从O(N*N!)变成O(N!).

https://leetcode-cn.com/problems/n-queens/solution/nhuang-hou-by-leetcode/

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        # 还是用backtrack看看
        # 对角线其实是两根交叉的直线，斜率分别为1和-1. 刚好匹配为i + j为常数和i - j为常数，不在两条线上的点则有不同的常数。
        
        def backtrack(sel_row, sel_cols, cross_i, cross_ii, seq, rv):
            if sel_row == n:
                rv.append(seq[:])
  
            for j in range(n):
                if j in sel_cols:
                    continue 
                if sel_row + j in cross_i or sel_row - j in cross_ii:
                    continue 
                seq.append((sel_row, j))  # 选择的位置
                sel_cols.add(j)  # 已经选择的col
                cross_i.add(sel_row + j)  # 右上斜线
                cross_ii.add(sel_row - j) # 右下斜线
                backtrack(sel_row + 1, sel_cols,cross_i, cross_ii, seq, rv)
                cross_ii.remove(sel_row - j)
                cross_i.remove(sel_row + j)
                seq.pop()
                sel_cols.remove(j)

        def transform(seq):
            matrix = [['.'] * n for _ in range(n)]
            for i, j in seq:
                matrix[i][j] = 'Q'
            rv = [''.join(col) for col in matrix]
            return rv

        col = []    
        backtrack(0, set(), set(), set(), [], col)
        
        rv = []
        for seq in col:
            rv.append(transform(seq))
        return rv 

执行用时：56 ms, 在所有 Python3 提交中击败了93.44%的用户
内存消耗：14 MB, 在所有 Python3 提交中击败了10.00%的用户

First Try

note: 提示错误，其实是横竖和斜线延伸都可以吃掉棋子，而不是只有7步的限制。

2020-07-28

N皇后问题听过很多次了，不过从来没有仔细去看下是什么难题，类似的记得还有个汉诺塔之类的入门级递归题目。

看到题目的时候感觉有点懵逼，暴力遍历这复杂度可能有点高。但是毕竟每行每列都只能选择一个，已经减少了很多冗余，其次再用交叉斜角排除掉被占用的位置，可能用暴力回溯递归法可以通过。

不管三七二十一，选择用backtrack回溯算法暴力遍历一波，结果竟然直接通过了，真是万能的回溯递归。

考虑的细节：每一行或者每一列都只能有一个元素，因此不用for i in range(rows): for j in range(cols)，直接row id每次加1就行，而col id则在n个位置里面随意选择一个，这样可以有效剔除重复选择。第一行有N列可以选择，第2行有N-1列可以选择，因此时间复杂度差不多是O(N!)。

剩下的复杂度在于选择斜角元素，用了最朴素的暴力写法，也是O(N)的复杂度。这样算起来复杂度其实差不多在O(N * N!)左右。由于斜角元素可能存在重复，因此没法使用简单的backtrack进行还原，这里每次都复制使用新的set进行处理，不需要还原了。

Anyway, 没想到第一次遇到这个传说中的经典题目直接就ac了，不错不错。

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        # 还是用backtrack看看
        
        def forbidden_slope(i, j):
            # 这个应该可以提前截获进行简化
            s = set([(i, j)])
            step = 0 
            while step <= n: 
                surroundings = [(i - step, j + step), (i + step, j + step), 
                                (i - step, j - step), (i + step, j - step)]
                s.update(set(surroundings))
                step += 1
            
            s = set([(i, j) for i, j in s if 0 <= i < n and 0 <= j < n])
            return s 
        
        def backtrack(sel_row, sel_cols, forbidden_set, seq, rv):
            if sel_row == n:
                rv.append(seq[:])
  
            for j in range(n):
                if j in sel_cols:
                    continue 
                if (sel_row, j) in forbidden_set:
                    continue 
                seq.append((sel_row, j))
                sel_cols.add(j)
                new_forbidden_set = forbidden_set.union(forbidden_slope(sel_row, j))
                backtrack(sel_row + 1, sel_cols, new_forbidden_set, seq, rv)
                seq.pop()
                sel_cols.remove(j)

        def transform(seq):
            matrix = [['.'] * n for _ in range(n)]
            for i, j in seq:
                matrix[i][j] = 'Q'
            rv = [''.join(col) for col in matrix]
            return rv

        col = []    
        backtrack(0, set(), set(), [], col)
        
        rv = []
        for seq in col:
            rv.append(transform(seq))
        return rv 

执行用时：228 ms, 在所有 Python3 提交中击败了7.89%的用户
内存消耗：14 MB, 在所有 Python3 提交中击败了10.00%的用户

51. N皇后 [hard]​

Second Try​

First Try​

51. N皇后 [hard]

Second Try

First Try