84. 柱状图中最大的矩形 [hard]

https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

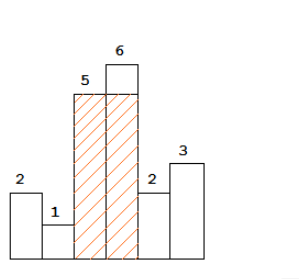
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

通过次数73,925 | 提交次数179,492

First Try

2020-07-27

使用单调递增栈，参考暴力解法里的思路，选择当前元素为顶的时候，能够构建的最大矩形面积。不过着眼点不是当前新加入的元素，而是栈顶元素。

如果遇到比栈顶元素大的元素，则放到栈里等待处理。
遇到比栈顶元素小的当前元素，则可以处理栈顶元素:
1. 对于栈顶元素而言，这是往右边走第一个比它小的元素。对以栈顶元素作为顶部的矩形来说，右边界确定了， -1。
2. 对于栈顶元素而言，其左边是往左边走第一个比它小的元素，因此左边界也确定了， +1.
3. 如果处理完后，栈里还有元素，可以考虑添加额外多一个0，肯定可以把该栈清空。
比较麻烦的是，在单调栈的时候遇到相等的元素该如何处理？单调栈不能保存相等元素，每次都pop out出来处理，但是计算后得到的size总归会小于下一个相等元素，因此对结果没有影响。
还有另一个角度可以考虑单调栈的选择，从左到右的时候，如果遇到某个元素比较小，那么前面比它大的元素的上面那一块都不会被用到了，只会用到当前元素的高度部分。因此扔掉较高的元素，并不会对结果造成影响。

最后重点再强调下：着眼点不是当前新加入的元素，而是在遇到新元素时候的栈顶元素。

参考题解得到的思路，其他题解真是看不下去： https://leetcode-cn.com/problems/largest-rectangle-in-histogram/solution/84-by-ikaruga/

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:

        stack = []
        heights.append(0)
        maxs = 0 
        for i in range(len(heights)):
            if not len(stack):
                stack.append(i) # 储存idx即可，毕竟数值通过heights[i]直接获取
                continue 
            stack_top = heights[stack[-1]]  # 写成了stacktop = stack[-1]，导致出错
            # 相等的元素果然头疼, 扔掉上一个，保留当前这个
            # if stack_top == heights[i]:  # 相等的元素并不会影响判断，直接扔掉。 <- 错误
            #     continue 
            # 这个其实没问题了，但还是放在>= heights[i]处处理吧
            # if stack_top == heights[i]:
            #     stack.pop()
            #     stack.append(i)
            #     continue 
            if stack_top < heights[i]:
                stack.append(i)
            # 最后一个可能就是stack[-1] > heights[i]了，但一路迭代修改为单调递增栈
            while stack_top >= heights[i]:  # 等号成立的前提是，如果存在多个重复的元素，总归最早的重复元素数值最大
                curr = stack.pop()
                rightmost = i - 1 
                leftmost = stack[-1] + 1 if len(stack) > 0 else 0  # 没有比它小的话，就给个0吧，起点
                size = (rightmost - leftmost + 1) * heights[curr]
                maxs = max(maxs, size)
                stack_top = heights[stack[-1]] if len(stack) else -1 # 终止
            # 前面都比当前元素小了，还是要把当前元素放到栈里
            stack.append(i)
        return maxs 

执行用时：112 ms, 在所有 Python3 提交中击败了5.60%的用户
内存消耗：15.9 MB, 在所有 Python3 提交中击败了11.11%的用户

Timeout Version

2020-07-27

至少得搞一个解法，就算是O(N^2)。

不管如何，最大面积的矩形，其顶部一定是某一根柱子的顶部
化整为零，考虑每根柱子作为顶部的矩形面积，然后进行比较。
之前要考虑可能矩形的各种变化，有点头疼。化整为零之后，整个思路就变得简单多了。

还是超时了，一个278长度的递增递减数列，超时的个例执行只用48ms，只是不让通过。

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        # 至少得搞一个解法，就算是O(N^2)。
        # 不管如何，最大面积的矩形，其顶部一定是某一根柱子的顶部
        # 化整为零，考虑每根柱子作为顶部的矩形面积，然后进行比较。
        # 之前要考虑可能矩形的各种变化，有点头疼。化整为零之后，整个思路就变得简单多了。
        # 还是超时了，一个278长度的递增递减数列，超时的个例执行只用48ms，只是不让通过
        maxsize = 0 
        for i in range(len(heights)):
            # 就算是相同高度，但可能在被分隔开的不同端，因此仍然需要来测试
            # if heights[i] in visited_h:  
            #     continue
            size_i = heights[i] 
            left, right = i - 1, i + 1 
            while left >= 0 and heights[left] >= heights[i]:
                size_i += heights[i]
                left -= 1
            while right <= len(heights) - 1 and heights[right] >= heights[i]:
                size_i += heights[i]
                right += 1
            maxsize = max(maxsize, size_i)
        return maxsize
            

84. 柱状图中最大的矩形 [hard]​

First Try​

Timeout Version​

84. 柱状图中最大的矩形 [hard]

First Try

Timeout Version