5465. 子树中标签相同的节点数 [medium]
5465. 子树中标签相同的节点数 [medium]
周赛198
通过的用户数516
尝试过的用户数1301
用户总通过次数516
用户总提交次数2004
题目难度Medium
给你一棵树(即,一个连通的无环无向图),这棵树由编号从 0 到 n - 1 的 n 个节点组成,且恰好有 n - 1 条 edges 。树的根节点为节点 0 ,树上的每一个节点都有一个标签,也就是字符串 labels 中的一个小写字符(编号为 i 的 节点的标签就是 labels[i] )
边数组 edges 以 edges[i] = [ai, bi] 的形式给出,该格式表示节点 ai 和 bi 之间存在一条边。
返回一个大小为 n 的数组,其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。
树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。
示例 1:
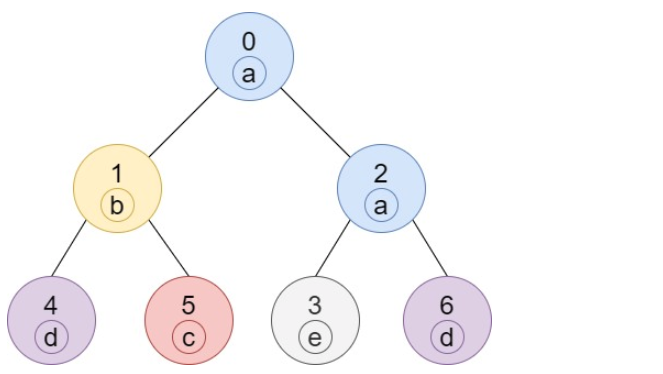
输入:n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出:[2,1,1,1,1,1,1]
解释:节点 0 的标签为 'a' ,以 'a' 为根节点的子树中,节点 2 的标签也是 'a' ,因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ,节点 1 的子树包含节点 1、4 和 5,但是节点 4、5 的标签与节点 1 不同,故而答案为 1(即,该节点本身)。
示例 2:
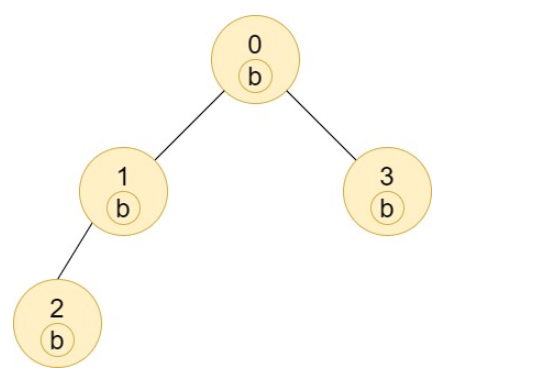
输入:n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出:[4,2,1,1]
解释:节点 2 的子树中只有节点 2 ,所以答案为 1 。
节点 3 的子树中只有节点 3 ,所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ,标签都是 'b' ,因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3,标签都是 'b',因此答案为 4 。
示例 3:
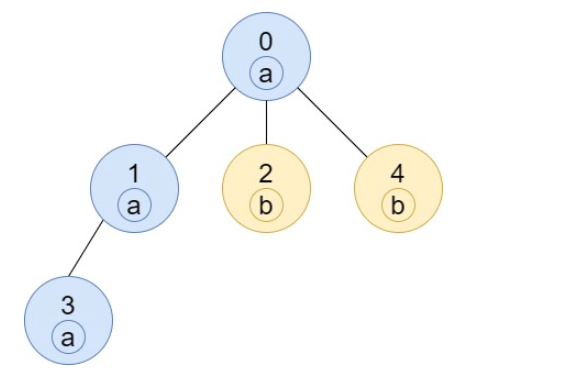
输入:n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出:[3,2,1,1,1]
示例 4:
输入:n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
输出:[1,2,1,1,2,1]
示例 5:
输入:n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
输出:[6,5,4,1,3,2,1]
提示:
- 1 <= n <= 10^5
- edges.length == n - 1
- edges[i].length == 2
- 0 <= ai, bi < n
- ai != bi
- labels.length == n
- labels 仅由小写英文字母组成
First Try
2020-07-19
本来题目不难,也是做过好几次类似的题目了,但是在题目的理解上贡献了好几次错误。
首先看图例发现并不是二叉树,开始把思路转化为图,就到了熟悉的递归领域。
其次以为edge指示了上级节点到下级,并且从0开始能一直遍历所有。 结果测试过程发现除了0之外,还有其他点没有被上级指向,于是以为这是一个多起点的图。
用indegree判断出多个起点之后,发现还会错误,这个就很难理解了。
后来对照着测试解看来看去,唯一可能的解释就是起点确实只有0,但是edge的方向需要自己判断,题目只是提供了边的信息而已。
比如这个测试案例,画出图来会以为是两个起点(0和1),但其实1是在2下面。
4
[[0,2],[0,3],[1,2]]
"aeed"
[1,1,2,1]
于是在构建图的时候在双向都添加上了节点,在递归过程中加上visited判断是否已经访问过,然后一路记录出现过所有字符的统计信息,于是终于搞定。
发现只要搞定了这道题(这才第二道),如果不是贡献了三次错误提交,在五千人的比赛中总成绩已经可以排到三百名内,获得微软内推机会了。 哎。
class Solution:
def countSubTrees(self, n: int, edges: List[List[int]], labels: str) -> List[int]:
# 这不是树,这是图吧
# 无环无向图,就是说没有方向的,只有一个root顶点。 我还以为有几个不同顶点,浪费了好几次错误提交。。
graph = collections.defaultdict(list)
# indegree = [0] * (n)
for s, e in edges:
graph[s].append(e)
graph[e].append(s)
# indegree[e] += 1
# roots = []
# for idx, i in enumerate(indegree):
# if i == 0:
# roots.append(idx)
# print('roots', roots)
# print('graph', graph)
def update_counter(c1, c2):
for k, v in c2.items():
c1[k] += v
cache = dict()
visited = set()
def dfs(node):
counter = collections.defaultdict(int)
counter[labels[node]] += 1
visited.add(node)
for c in graph[node]:
if c in visited:
continue
update_counter(counter, dfs(c))
# print('node', node, "counter", counter)
cache[node] = counter
return counter
# for r in indegree:
# dfs(r)
dfs(0)
# print(cache)
rv = []
for i in range(n):
rv.append(cache[i][labels[i]])
return rv
# ### 预期
# 4
# [[0,2],[0,3],[1,2]]
# "aeed"
# [1,1,2,1]