5477. 排布二进制网格的最少交换次数 [medium]

5477. 排布二进制网格的最少交换次数 [medium]

第 200 场周赛, paypal专场

https://leetcode-cn.com/contest/weekly-contest-200/problems/minimum-swaps-to-arrange-a-binary-grid/

给你一个 n x n 的二进制网格 grid，每一次操作中，你可以选择网格的 相邻两行 进行交换。

一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。

请你返回使网格满足要求的最少操作次数，如果无法使网格符合要求，请你返回 -1 。

主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。

示例 1：

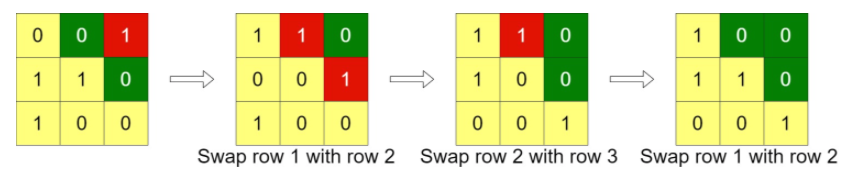
输入：grid = [[0,0,1],[1,1,0],[1,0,0]]
输出：3

示例 2：

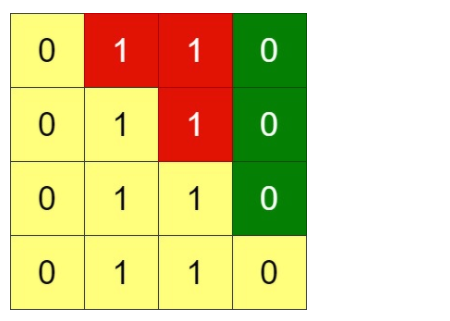
输入：grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
输出：-1
解释：所有行都是一样的，交换相邻行无法使网格符合要求。

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,1]]
输出：0

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 200
• grid[i][j] 要么是 0 要么是 1 。

Failed Try

2020-08-02

没有做出来, 最后超时了。

做了半个小时后，发现题目看错了，是对角线以上的元素为0，而不是对角线上的元素为0。但这并不影响做题过程，因为还是没做出来。

考虑使用backtrack遍历所有位置的所有可能，然后再统计移动邻边的次数。实在没想到怎么统计，后来取巧用暴力排序法来模拟，每次遇到顺序不对的，就交换相邻元素，没交换一次就统计一次，最后得到排序的数组所需要的交换次数就是邻边移动次数。

但是还是超时了，得第二天看放出来的题解了。

class Solution:
    def minSwaps(self, grid: List[List[int]]) -> int:
        # 麻烦的是如何邻边交换。。。
        # 先动手看看
        n = len(grid)
        choices = collections.defaultdict(list)
        for i in range(n):
            for j in reversed(range(n)):
                choices[j].append(i)
                if grid[i][j] == 1:
                    # choices[n - 1 - (n - 1 - j)].append(j)
                    # choices[j].append(i)
                    break

            
        
        print(choices)

        if len(choices) < n:
            return -1 
        choices = [choices[i] for i in range(n)]
        
        
        def backtrack(idx, seq, visited, rv):
            if idx == n:
                rv.append(seq[:])
                return 
            for c in choices[idx]:
                if c in visited:
                    continue 
                seq.append(c)
                visited.add(c)
                backtrack(idx + 1, seq, visited, rv)
                visited.remove(c)
                seq.pop()
        rv = []
        backtrack(0, [], set(), rv)
        print(rv)
        
        if not len(rv):
            return -1
        
        def cal_steps(arr):
            # 冒泡排序法的次数统计。。
                    
            counter = 0 
            flag = False 
            while not flag:
                flag = True 
                for i in range(0, len(arr) - 1):
                    if arr[i] > arr[i + 1]:
                        arr[i], arr[i + 1] = arr[i + 1], arr[i]
                        counter += 1
                        flag = False 
            return counter 
        
        def cal_steps(arr):
            counter = 0           
            i = 0 
            while i < n:
                j = i 
                while n - 1 > j >= 0 and arr[j] > arr[j + 1]:
                    arr[j], arr[j + 1] = arr[j + 1], arr[j]
                    j -= 1 
                    counter + 1
                i += 1 
            return counter 
              
        steps = [cal_steps(r) for r in rv]
        return min(steps)