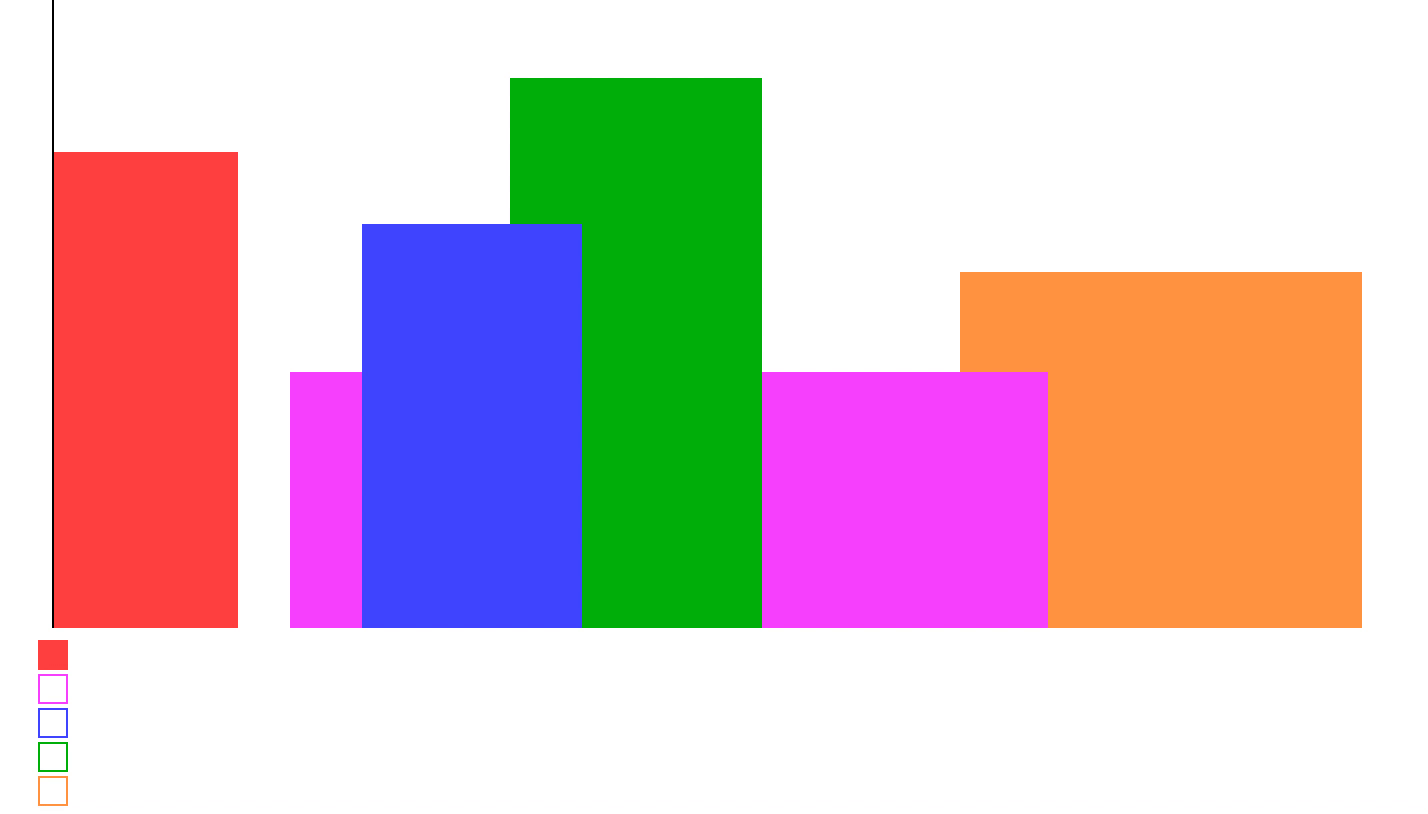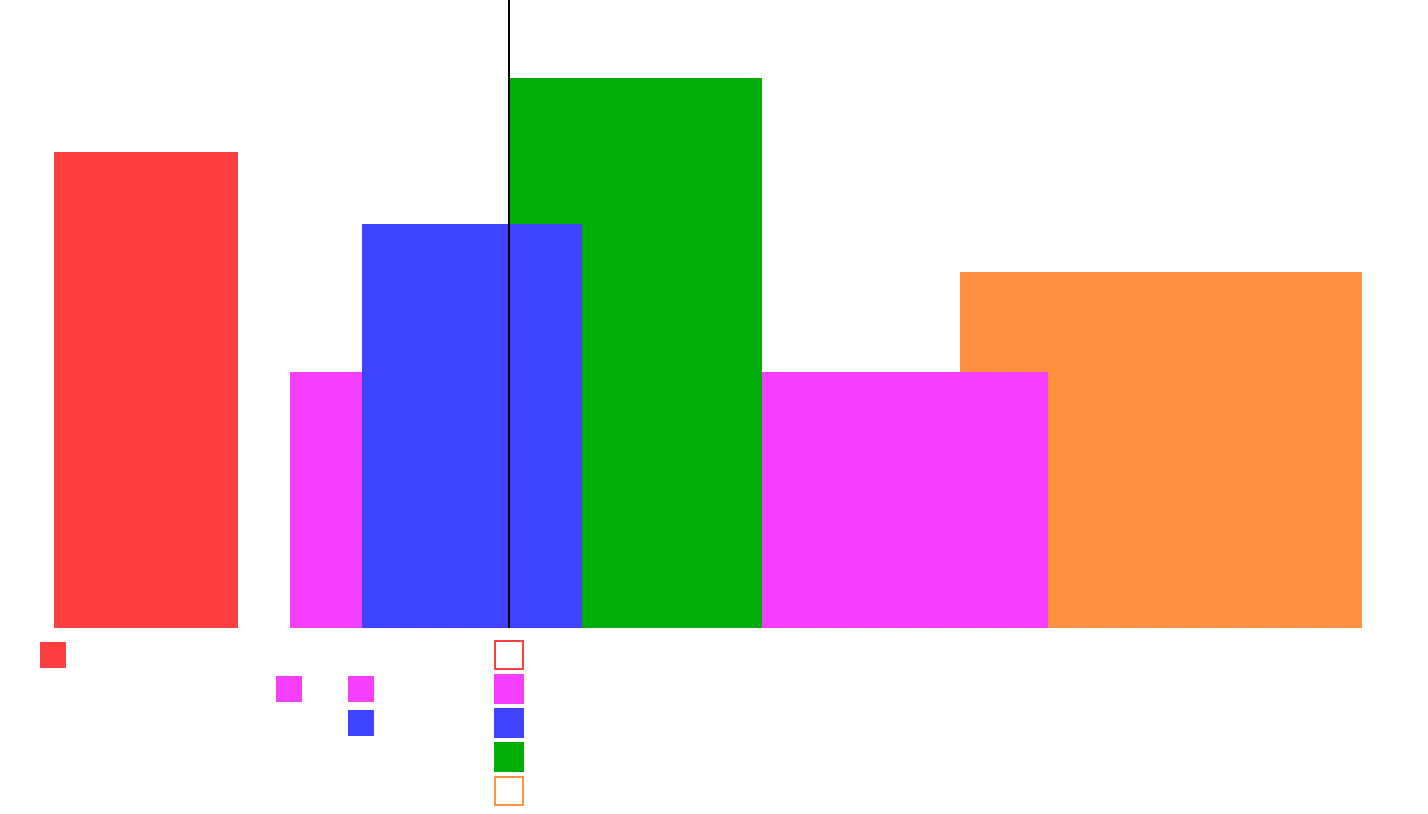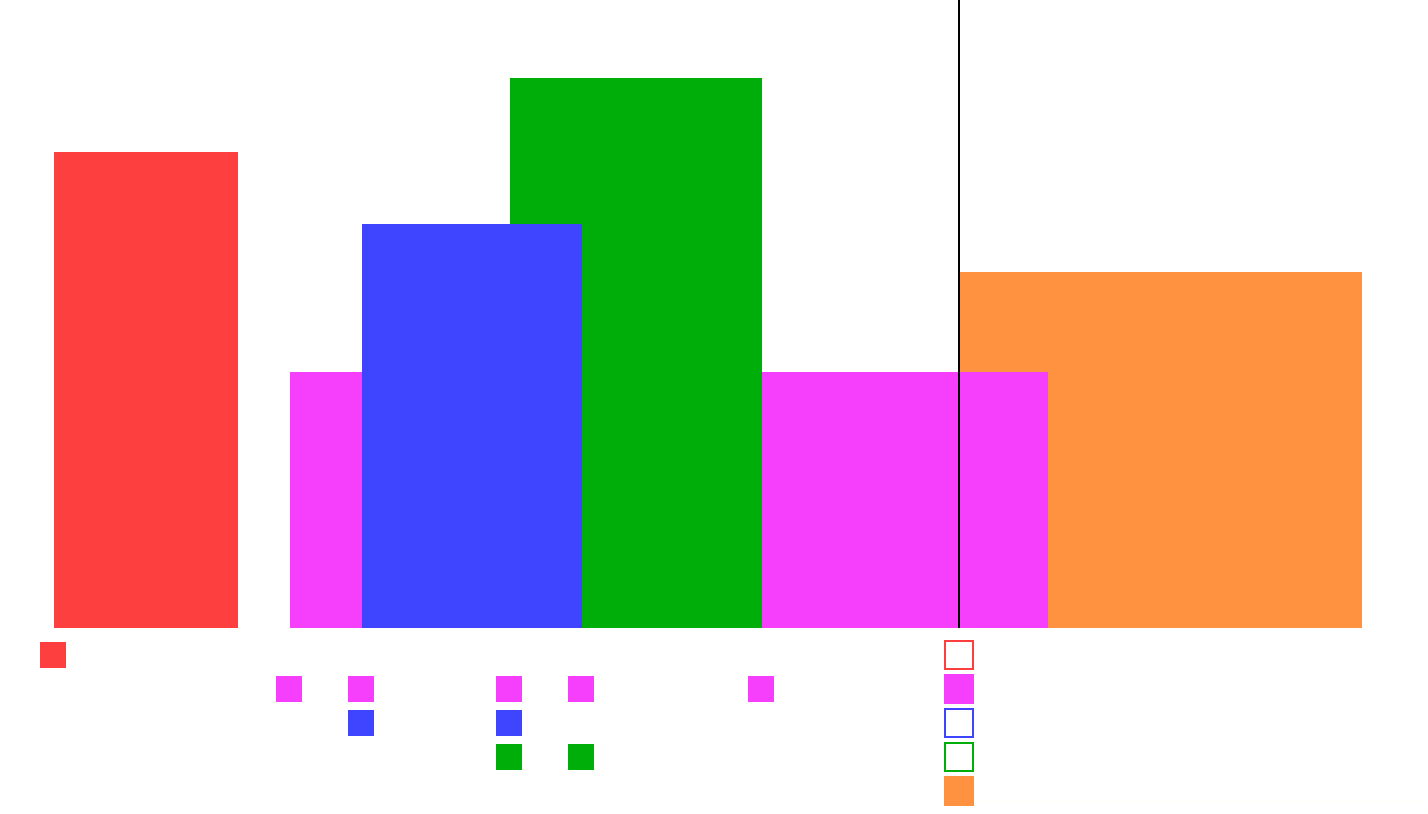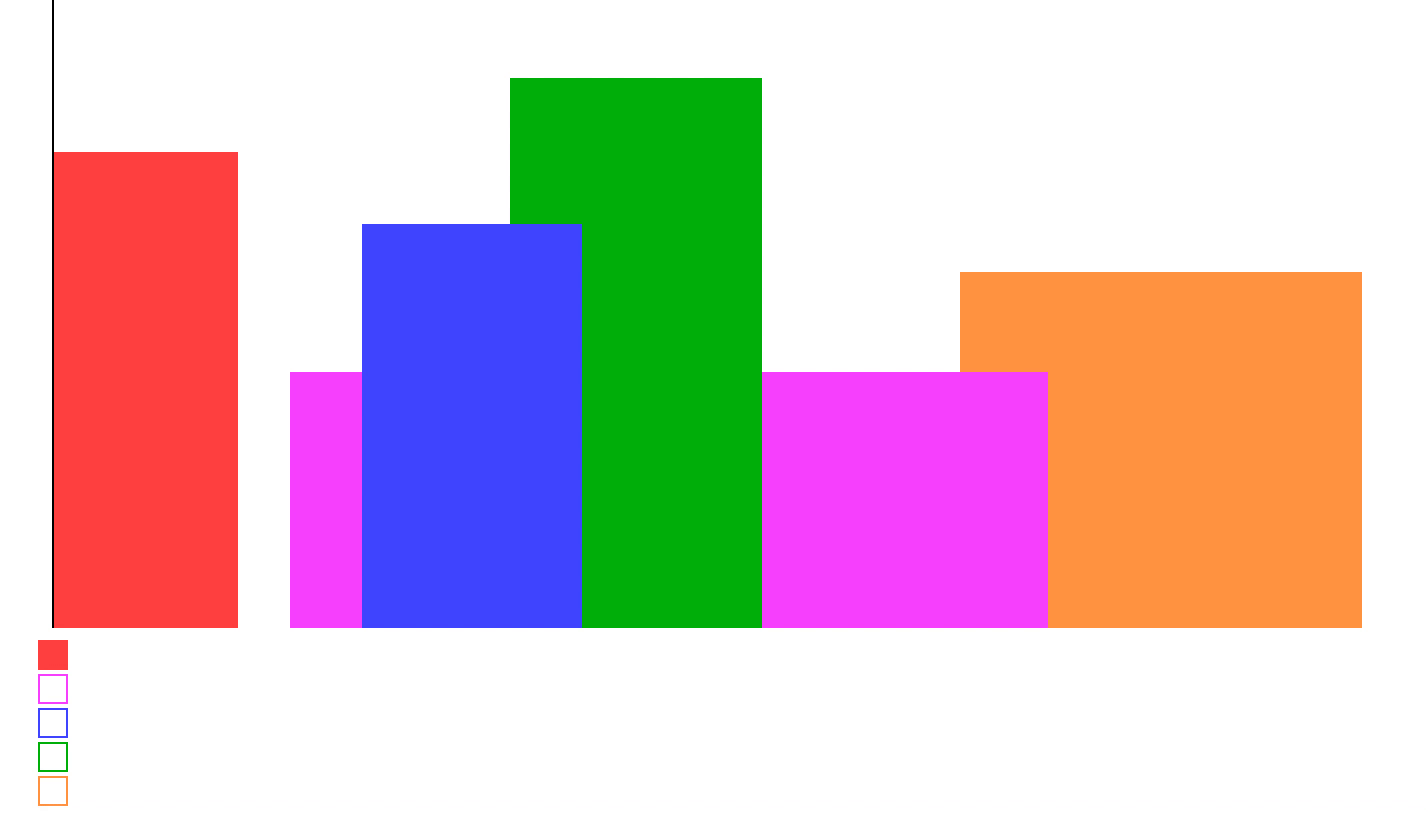218. 天际线问题 [hard]
218. 天际线问题 [hard]
https://leetcode-cn.com/problems/the-skyline-problem/
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。
Buildings Skyline Contour
每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。
例如，图A中所有建筑物的尺寸记录为：[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。
输出是以 [ [x1,y1], [x2, y2], [x3, y3], ... ] 格式的“关键点”（图B中的红点）的列表，它们唯一地定义了天际线。关键点是水平线段的左端点。请注意，最右侧建筑物的最后一个关键点仅用于标记天际线的终点，并始终为零高度。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
例如，图B中的天际线应该表示为：[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。
说明:
- 任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
- 输入列表已经按左 x 坐标 Li 进行升序排列。
- 输出列表必须按 x 位排序。
- 输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]
通过次数8,181 | 提交次数19,038
Second Try
2020-07-16
这是一个比较纠结的版本，思路没有first try里的那么直接。 前面的一样，重点是解决每一轮判断当前重叠楼层的最高高度上面，使用了优先队列。
由于python优先队列为极小堆，因此取反直接变成极大堆。对高度取反的操作，刚好是一个优化必备的内容，这样就不用考虑在同一个坐标点有两个不同高度的进来，两个出去，一个进来一个出去的问题。具体看first try里面improved version里的分析。
其次对于每一个进来的元素，都记录了start和end的位置。在遇到需要剔除的点的时候，考虑的是极小值是否有效，也就是end的位置是否比当前idx还要早，若是早的话直接扔掉。本来应该是仔细剔除匹配的那个点，但优先队列删除特定元素简直相当于重新排列一遍O(nlgn),那就没必要了。因此这是一个取巧的方法，但能够解决问题。
于是，在两个tricks的带领下一波解决问题。
剔除无效点的方法，隐隐约约记得前面的某道题也有用类似的思路，但要一次性考虑到这个解法还是有点难度。。。
class Solution(object):
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
# 用max方式还是太慢了，还是想搞成堆的方式，只删除能够删除的，未能删除的并不能被获取到，不管
if not (buildings and buildings[0]):
return []
seq = []
for start, end, height in buildings:
seq.append([start, -height, end])
seq.append([end, height, 0])
seq = sorted(seq)
rv = []
preh = 0
heap = []
for idx, height, ridx in seq:
# print("preheq", heap, "idx, height", idx, height)
if height < 0:
heapq.heappush(heap, [height, ridx]) # 取负值适应极小堆
elif height > 0:
while len(heap) and heap[0][1] <= idx: # 选取idx而非ridx
heapq.heappop(heap) # 虽然可能有漏网之鱼，但当前只关心heap-max点，已经剔除了该扔掉的建筑
max_height, ridx = heap[0] if heap else [0, ridx]
# print("after heap", heap, "idx height", idx, height, ridx, "preh", preh, "maxh", max_height)
if max_height != preh:
rv.append([idx, -max_height])
preh = max_height
return rv
- 执行用时：60 ms, 在所有 Python 提交中击败了64.94%的用户
- 内存消耗：18.5 MB, 在所有 Python 提交中击败了50.00%的用户
First Try
2020-07-16
复杂度差不多算是O(N^2)吧，总共n个循环，每个循环要寻找max(slots),极端情况下又是N，因此是O(N^2)。看题解max(slots)阶段用的是红黑树之类，可以快速确定极大值并且移除某个点，因此是O(NlgN)的复杂度。
这篇题解的gif图形讲解的非常好: https://leetcode-cn.com/problems/the-skyline-problem/solution/218tian-ji-xian-wen-ti-sao-miao-xian-fa-by-ivan_al/
还是得用之前看过得一种解法，该长度内只考虑起点和尾点。为了能够获取何时往下走，需要对起点和尾点分别进行排序。遍历过程中，每次遇到节点的时候，对当前重叠部分的楼层进行操作，然后判断当前重叠部分的楼层的最高高度，与上一个节点的最高高度进行判断，如果有区别就把该点记作关键点。
理解的关键是对节点遍历过程中，考虑当前重叠的楼的最高高度。
class Solution(object):
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
# 还是得用之前看过得一种解法，该长度内只考虑起点和尾点。为了能够获取何时往下走，需要对起点和尾点分别进行排序才行。
if not (len(buildings) and len(buildings[0])):
return []
seq = [] # [index, height]
for start, end, height in buildings:
seq.append([start, height])
seq.append([end, -height])
seq = sorted(seq)
rv = []
slots = []
prev_h = 0
i = 0
# 需要考虑到同一个位置有多个不同的楼层上升下降，用迭代法就没法考虑到这种情况，只能用两层while
while i < len(seq):
j = i
while j < len(seq) and seq[j][0] == seq[i][0]: # 第一个肯定中招
idx, height = seq[j]
if height < 0:
slots.remove(-height)
elif height > 0:
slots.append(height)
i = j
j += 1
curr_h = max(slots) if len(slots) else 0
if curr_h != prev_h:
rv.append([idx, curr_h])
prev_h = curr_h
i += 1
return rv
- 执行用时：632 ms, 在所有 Python 提交中击败了14.29%的用户
- 内存消耗：17.5 MB, 在所有 Python 提交中击败了100.00%的用户
- improved version
将height取负数，可以避免同一个位置不同高度开始和结束的问题，仔细思考会发现很巧妙，但我不觉得未经训练还能一次性写出这个tricks.
比如height为负的时候，排序的时候，同一个idx位置越高的排在前面，进来的排在出去的前面。考虑两个不同高度的进来，两个不同高度的出去，一个进来一个出去这三种情况，会发现刚好完美解决。这样就不需要双重while进行前溯了。
class Solution(object):
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
# 还是得用之前看过得一种解法，该长度内只考虑起点和尾点。为了能够获取何时往下走，需要对起点和尾点分别进行排序才行。
if not (len(buildings) and len(buildings[0])):
return []
seq = [] # [index, height]
for start, end, height in buildings:
seq.append([start, -height])
seq.append([end, height])
seq = sorted(seq)
rv = []
slots = []
prev_h = 0
i = 0
# 需要考虑到同一个位置有多个不同的楼层上升下降，用迭代法就没法考虑到这种情况，只能用两层while
# 但是把height变成负数，就不需要考虑这个问题了
while i < len(seq):
idx, height = seq[i]
# print("slots", slots, idx, height)
if height > 0:
slots.remove(-height)
elif height < 0:
slots.append(height)
curr_h = -min(slots) if len(slots) else 0
if curr_h != prev_h:
rv.append([idx, curr_h])
prev_h = curr_h
i += 1
return rv
- 执行用时：1480 ms, 在所有 Python 提交中击败了7.79%的用户
- 内存消耗：17.7 MB, 在所有 Python 提交中击败了100.00%
- failed try
无脑暴力解法，遇到测试集[[0,2147483647,2147483647]]直接内存超标了。
# 内存崩溃版
class Solution(object):
def getSkyline(self, buildings):
"""
:type buildings: List[List[int]]
:rtype: List[List[int]]
"""
# 两轮循环比较容易一些
# 在起始点+h, 在结束点-h，这样方便了许多
# 写不出来，用了暴力法，果然内存超标了
# [[0,2147483647,2147483647]]
if not (len(buildings) and len(buildings[0])):
return []
start = buildings[0][0]
end = max(buildings, key=lambda x: x[1])[1]
# print('start', start, "end", end)
cache = [0] * (end + 1) # 额外多一个
for (st, ed, height) in buildings:
for i in range(st, ed): # 有效的是[st, ed - 1], 并不包括最后一个的ed
cache[i] = max(cache[i], height)
rv = [[start, cache[start]]]
# print("cache", cache)
for i in range(start + 1, end + 1):
if cache[i] != cache[i - 1]:
rv.append([i, cache[i]])
return rv