1514. 概率最大的路径 [medium]

https://leetcode-cn.com/problems/path-with-maximum-probability/

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：

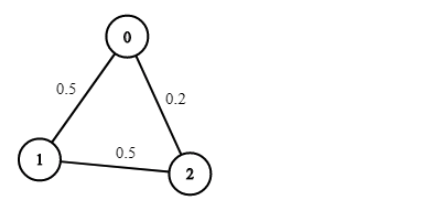
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

示例 2：

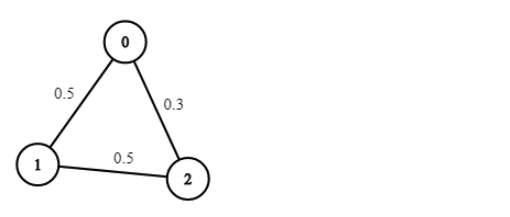
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000

示例 3：

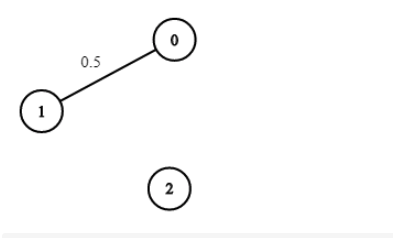
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

提示：

2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边

通过次数2,655 | 提交次数11,279

First Try

2020-07-15

dijstra 最短路径算法的另一个反向应用，优先队列修改为最大优先队列，然后每轮都抓去从起点开始最大概率先到的线路就行（与prim不同，prim最小生成树是每一轮都抓取离当前树最近距离的点），因此放进去的概率是所有前面路径概率的乘积。

python的heapq是最小堆，因此需要把概率都转化为负值再进行处理。

import heapq
class Solution(object):
    def maxProbability(self, n, edges, succProb, start, end):
        """
        :type n: int
        :type edges: List[List[int]]
        :type succProb: List[float]
        :type start: int
        :type end: int
        :rtype: float
        """
        # dijkstra算法
        # python的heap为最小堆，因此概率都取反，最小负值就是最大正值
        graph = collections.defaultdict(list)
        for i, (ni, nii) in enumerate(edges):
            graph[ni].append([-succProb[i], nii])
            graph[nii].append([-succProb[i], ni])
        heap = [[-1, start]] # 毕竟start开始，因此概率为1
        visited = set() # 已经被提前访问过的话就不能再被访问了
        while len(heap):
            prob, node = heapq.heappop(heap)
            if node == end:
                return -prob 
            if node in visited:
                continue
            visited.add(node)
            for p, n in graph[node]:
                if n in visited:
                    continue 
                heapq.heappush(heap, [-prob * p, n])
        return 0 

执行用时：296 ms, 在所有 Python 提交中击败了62.16%的用户
内存消耗：26.3 MB, 在所有 Python 提交中击败了100.00%

1514. 概率最大的路径 [medium]​

First Try​

1514. 概率最大的路径 [medium]

First Try