164. 最大间距 [hard]

https://leetcode-cn.com/problems/maximum-gap/

给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。

如果数组元素个数小于 2，则返回 0。

示例 1:

输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。

示例 2:

输入: [10]
输出: 0
解释: 数组元素个数小于 2，因此返回 0。

说明:

你可以假设数组中所有元素都是非负整数，且数值在 32 位有符号整数范围内。
请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。

通过次数16,109 | 提交次数29,154

Third Try

2020-07-15

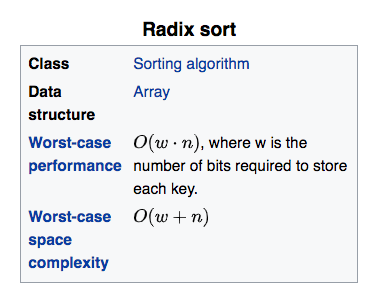
传说中的基数排序，radix sort

看官方题解总是理解不了，看百度里的python例子终于能够自己写一个，但还是理解不了题解里奇怪的写法。

首先用log求出最大值的位数，按位循环需要的数量就是最大数值的位数
通过 val // (10 ** i) % 10 求取第i + 1位的数值，比如可以替代i=0的时候，求得个位数的数值，也即第1位的数值
第一轮排序把个位数相同的都放一起，之后汇总更新原数组，结果是个位数越大的排越后，个位数相同的前后关系并不考虑。
第二轮排序，如果十位数相同，那么由于在第一轮中按照个位数排序，结果是个位数越大的，排位越后
第三轮，第四轮，第n轮同理，每一轮如果遇到相同位数的，则由n-1轮的位数决定。
在第n轮的时候，如果其他数字长度都小于n，那么其他数字都放在第一个bucket中，只有长度大于等于n的数字可能放在任意一个bucket中，但就算放在第一个，仍然会比前面的排在后面（如果长度仅为n，那么其实最大位不可能是0，但不影响分析）
bingo, radix sort问题解决。

复杂度不好说啊，毕竟最后nums也已经是排序完毕了，总不可能是O(n)吧。

百度：基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数。

https://en.wikipedia.org/wiki/Radix_sort

https://leetcode-cn.com/problems/maximum-gap/solution/zui-da-jian-ju-by-leetcode/

class Solution(object):
    def maximumGap(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        # 基数排序，这要是可以，其他排序岂不是也可以这么玩
        if len(nums) < 2:
            return 0 

        maxv, minv = max(nums), min(nums)
        kdigits = int(math.log10(maxv)) + 1
        buckets = [[] for _ in range(10)]
        # print("kdigits", kdigits)
        for i in range(0, kdigits):
            # print("digits before: ", i, "nums", nums)
            for n in nums:
                buckets[n // (10 ** i) % 10].append(n)
            nums_sorted_k_digit = []
            for b in buckets:
                nums_sorted_k_digit.extend(b)
            # 更新数组和bucket，数组按第i位进行排序
            nums = nums_sorted_k_digit
            buckets = [[] for _ in range(10)] 
            # print("digits after: ", i, "nums", nums)

        # print("buckets", buckets)
        # print("nums", nums)
        # 其实这时候nums已经是排序后的数组，一轮循环即可
        rv = 0
        for i in range(1, len(nums)):
            rv = max(rv, abs(nums[i] - nums[i - 1]))
        return rv 

执行用时：36 ms, 在所有 Python 提交中击败了41.09%的用户
内存消耗：13.2 MB, 在所有 Python 提交中击败了100.00%的用户

参考的radix sort 基数排序

import math

def sort(a, radix=10):
    """a为整数列表， radix为基数"""
    K = int(math.ceil(math.log(max(a), radix))) # 用K位数可表示任意整数
    bucket = [[] for i in range(radix)] # 不能用 [[]]*radix
    for i in range(1, K+1): # K次循环
        for val in a:
            bucket[val%(radix**i)/(radix**(i-1))].append(val) # 析取整数第K位数字 （从低到高）
        del a[:]
        for each in bucket:
            a.extend(each) # 桶合并
        bucket = [[] for i in range(radix)]

看不懂的官方题解radix sort基数排序

https://leetcode-cn.com/problems/maximum-gap/solution/zui-da-jian-ju-by-leetcode/

int maximumGap(vector<int>& nums)
{
    if (nums.empty() || nums.size() < 2)
        return 0;

    int maxVal = *max_element(nums.begin(), nums.end());

    int exp = 1;                                 // 1, 10, 100, 1000 ...
    int radix = 10;                              // base 10 system

    vector<int> aux(nums.size());

    /* LSD Radix Sort */
    while (maxVal / exp > 0) {                   // Go through all digits from LSD to MSD
        vector<int> count(radix, 0);

        for (int i = 0; i < nums.size(); i++)    // Counting sort
            count[(nums[i] / exp) % 10]++;

        for (int i = 1; i < count.size(); i++)   // you could also use partial_sum()
            count[i] += count[i - 1];

        for (int i = nums.size() - 1; i >= 0; i--)
            aux[--count[(nums[i] / exp) % 10]] = nums[i];

        for (int i = 0; i < nums.size(); i++)
            nums[i] = aux[i];

        exp *= 10;
    }

    int maxGap = 0;

    for (int i = 0; i < nums.size() - 1; i++)
        maxGap = max(nums[i + 1] - nums[i], maxGap);

    return maxGap;
}

复杂度分析

时间复杂度：O(d \cdot (n + k)) \approx O(n)O(d⋅(n+k))≈O(n)

由于在数组上的线性迭代是接近线性复杂度，所以方法的时间性能瓶颈只要是基数排序。

基数排序以计数排序为基础。

计数排序时间复杂度是 O(n+k)O(n+k)，其中 kk 是数组 nn 个元素的基数（数字个数）。如果 k \leq O(n)k≤O(n)，计数排序可以在线性时间内完成。在我们的例子中，基数是固定的（比如，k = 10k=10），因此计数排序运行时间是线性的 O(n)O(n)。基数排序运行 dd 轮计数排序（其中每个元素由最多 dd 个数字组成）。因此有效运行时间是 O(d \cdot (n + k))O(d⋅(n+k))，但在我们的例子中，最大可能的 32 位有符号是 2147483647，因此 d \leq 10d≤10 是常数。因此基数排序的时间效率是 O(n)O(n)。

空间复杂度：O(n + k) \approx O(n)O(n+k)≈O(n)额外空间。

计数排序需要额外 O(k)O(k) 空间，基数排序需要一个和输入数组相同大小的辅助数组。然而给定的 kk 是一个固定小常数，所以在大输入情况下计数排序的额外空间是可以被忽略的。

作者：LeetCode 链接：https://leetcode-cn.com/problems/maximum-gap/solution/zui-da-jian-ju-by-leetcode/ 来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Second Try

2020-07-15

使用bucket解法，思路是对于m个数组，如果分为m个bucket，并且第一个和最后一个都填充了元素，那么要么所有元素均匀分布，要么存在空的bucket。在前一种情况中，最大gap就是相邻bucket的数值差距。在后一种情况中，最大的gap就是空了最多bucket的前后两个bucket中的数值之差。

据说这个也叫鸽笼原理: nn 个物品放入 mm 个容器中，如果 n > mn>m 那么一定有一个容器装有至少两个物品。

问题是对于bucket的分组非常头疼。

比如对于下面的长度为4的数组:

普通的[2, 4, 6, 8]数组，判断bucket容量为(8 - 2) / (4 - 1) = 2, 数组为(2,3),(4,5),(6, 7), (8, 9), 刚好确实是4个bucket
普通的[1, 2, 3, 4]数组，判断bucket容量为(4 - 1) / (4 - 1) = 1, 数组为(1),(2), (3), (4),也刚好是4个bucket
来了一个[1, 3, 6, 9]数组，判断bucket容量为(9 - 1) / (4 - 1) = 2, 数组为(1, 2), (3, 4), (5, 6), (7, 8), (9, 10), 好了，竟然是5个bucket！

看题解有些人分析得头头是道，理得很清楚，有的地方额外加1即可。但我实在绕不出来，由于最后一个元素和第一个元素都要求在bucket中，因此直接用get_bucket_id(max_v)来处理最好了，世界又变得清晰了起来。

看了别人的题解，大家在算bucket num的时候，用的是 (maxv - minv) / bucket_size + 1, 因为桶内的区间都是前闭后开的，如果不额外多一个桶就包括最后一个元素。因此前面第一种情况是(8 - 2) / 2 + 1 = 4个bucket，第二种情况是(4 - 1) / 1 + 1 = 4个bucket，第三种情况是(9 - 1) / 2 + 1 = 5个bucket, bingo! 问题竟然解决了。

虽然解决了，但是还是没有完全把这边角思路处理好，以后再看吧，至少有安全解法了。

复杂的边边角角就让程序考虑好了，另外现在是m个元素的数组，分布在m或m+1个bucket中，而不是直接m个bucket了，但这并不影响问题的基础分析。

两轮扫描解决问题，属于O(N)复杂度，不错。

关于桶数量的解释：

作者：jerrymouse1998

链接：https://leetcode-cn.com/problems/maximum-gap/solution/javacong-bi-jiao-pai-xu-dao-ji-shu-pai-xu-zai-dao-/

桶排序也是计数排序的一种，普通的计数排序相当于极端情况下每个桶的区间大小是 1 ，而这里说的桶排序肯定不是这种极端情况，每个桶的区间大小相等，但依然是遍历元素对号入座(放入对应的区间里)。

桶排序的重点就在于，如何规划桶区间的大小和个数，使尽可能少的桶，去覆盖所有的元素。

规划桶大小和数量，必然要知道输入的区间，所以需要知道输入最大元素 max 、最小元素 min，从而知道输入区间总长度 max - min ，用 输入区间总长度/区间个数 得到桶的大小 bucketSize。（区间个数 = 元素个数 - 1）

有了桶的大小，就不难得到桶的数量 (max-min)/bucketSzie + 1 ，为什么要 +1 多一个桶呢？

因为桶内的区间都是前闭后开的，形如 [min,a)、[b,c)、[d,e)、[f,max)，所以如果不 +1 生成的桶将不包含边界值 max 。因此 +1 是为了方便编码，不需要单独去处理边界值 max 。

最后就是找最大间距了！这里需要用到抽屉定理的思想(在 NO.41 缺失的第一个正数 题目中也用到过这个思想)，最大间距一定 >= 输入区间大小/输入区间的数量！

我的代码

class Solution(object):
    def maximumGap(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        """
        草稿
        3 6 9 1
        1,3,6,9 -> gap = (9 - 1) // (4 - 1) =  2 -> 1-2, 3-4, 5-6, 7-8, 9, 差一个9 
        """
        # 来个线性时间的，只能是bucket分组了
        if len(nums) < 2:
            return 0 
        maxv, minv = max(nums), min(nums)
        if maxv == minv:  # 又一个bug, 但这样还不够，还得判断gap=max(1, gap)
            return 0 
        gap = (maxv - minv) // (len(nums) - 1)  # 取整的存在，导致其实gap偏小
        gap = max(1, gap)  # 至少为1,又是通过提交测试才发现的。。。比如该测试组: [1,1,1,1,1,5,5,5,5,5]
        bid = lambda x: (x - minv) // gap # 由于gap偏小，最后可能会导致bucket数量多一点？但是这个也是整数除法，不好说接下来是什么差别，f**k，这些细节
        bnum = bid(maxv) + 1  # 用最大值来确定bucket数量，因为实在想不懂什么时候是len(num),什么时候是len(num) + 1
        buckets = [[] for _ in range(bnum)]  # 对n个元素，使用m个bucket，要么bucket均匀分布，要么有间隔
        # print("max", maxv, "min", minv, "gap", gap, "n", len(nums), "bnum", bnum)
        for n in nums:
            # print("num", n," at bucket: ", bid(n))
            buckets[bid(n)].append(n)
        # print("buckets", buckets)
        prev = max(buckets[0])
        rv = 0
        for b in buckets[1:]:
            if len(b):
                rv = max(rv, min(b) - prev)
                prev = max(b)
        return rv 

执行用时：36 ms, 在所有 Python 提交中击败了41.09%的用户
内存消耗：14.2 MB, 在所有 Python 提交中击败了100.00%的用户

First Try

2020-07-15

非线性的，排序再取间隔，速度也还可以啊。

class Solution(object):
    def maximumGap(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        # 先来个非线性时间的
        nums = sorted(nums)
        maxv = 0
        for i in range(1, len(nums)):
            maxv = max(maxv, abs(nums[i] - nums[i-1]))
        return maxv 

执行用时：28 ms, 在所有 Python 提交中击败了66.67%的用户
内存消耗：13.1 MB, 在所有 Python 提交中击败了100.00%的用户