322. 零钱兑换 [medium]
322. 零钱兑换 [medium]
https://leetcode-cn.com/problems/coin-change
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明: 你可以认为每种硬币的数量是无限的。
通过次数90,962 | 提交次数228,560
Second Try
2020-06-10
由于每个元素都会被遍历一遍,因此可以从下往上走进行动态规划,不需要递归调用,看起来速度更快了。重点在于每个被遍历到的dp(n)点,所有小于n的点必然都已经被遍历过了。每次只要在所有coin硬币中,选择dp(n-x)为最小的值即可,最终dp(n) = dp(n-x) + 1即是最小的值。
最开始理解还是从上往下递归调用的方式比较容易理解,从下往上的写法,则容易绕进死胡同。理解关键在于从下往上走,需要意识到最终必然会走到n数值,而在n之前的任意数值并不考虑n这个最终的目标,大家都只是最好在自己数字内的最优选择而已,最终使得目标n能够得到最优解法。
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
if amount <= 0:
return 0
cache = {c: 1 for c in coins}
for i in range(1, amount + 1):
if i in cache:
continue
choices = []
for c in coins:
if i - c < 0 or (i - c) not in cache:
continue
choices.append(cache[i - c] + 1)
if len(choices):
cache[i] = min(choices)
return cache[amount] if amount in cache else -1
- 执行用时 :1156 ms, 在所有 Python 提交中击败了40.95%的用户
- 内存消耗 :13.9 MB, 在所有 Python 提交中击败了16.67%的用户
First Try
2020-06-10
非常经典的完全背包问题,可以选择任意无限的元素,因此每次循环中都需要考虑所有可能。第一次接触这种类型完全不会做,知道套路后就好了一些。分明看过《算法4》,但还是有这么多别人常见的套路不了解。
- 考虑最优的选择为DP(n), 最后一个元素为x, 则DP(n-x) + 1也是最优选择,一直不停递归到DP(0)起点,这一路就是选择的硬币。
- 但是此刻并不知道最后一个元素x具体是多少,需要遍历所有硬币的可能。不管选择的是哪一个,只要+1就是总次数,因此只要找到最小的DP(n-x),x即为最后一个元素。
- 由于每次DP(n)都顺利往下走,问题成功变成一个递归问题。由于n-x一路迭代存在各种重复,使用缓存矩阵进行加速,问题变成了一个动态规划问题。
- 考虑边界条件,base condition可以是所有硬币,也可以是从0开始。
- 如果递归到了最小值依然不是零,则返回-1
- 这是一个从上往下走的递归写法,second try中则为从下往上走的写法,不需要递归。
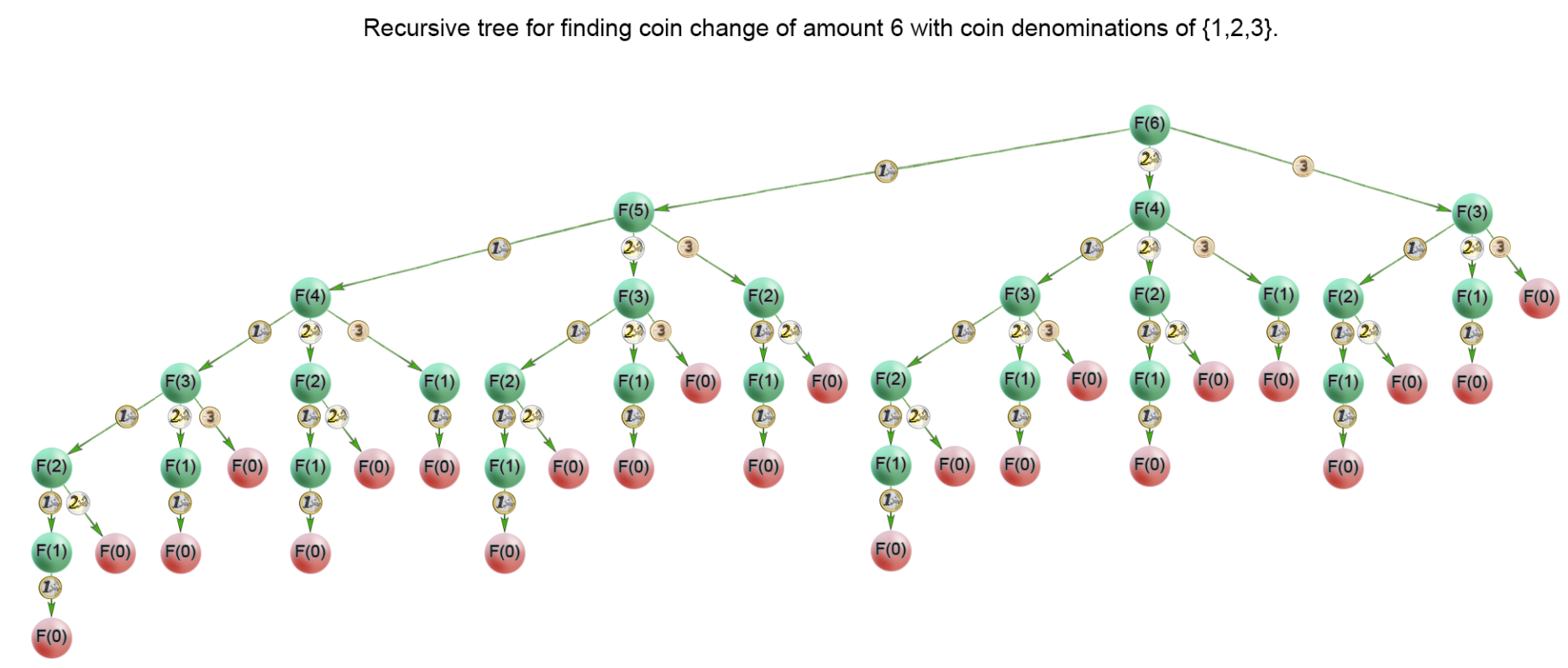
动态规划问题的理解:
- 【MIT公开课】麻省理工Erik Demaine动态规划系列课程(中英字幕+笔记): https://www.bilibili.com/video/BV1qt4y127pC?p=3
- 【动态规划】背包问题: https://www.bilibili.com/video/BV1K4411X766?from=search&seid=15047335386033912507
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
if amount < 1:
return 0
cache = {}
for c in coins:
cache[c] = 1
def dp(amount):
if amount in cache:
return cache[amount]
choices = []
for c in coins:
if amount < c or dp(amount - c) < 0:
continue
choices.append(dp(amount - c) + 1)
min_c = -1 if len(choices) == 0 else min(choices)
cache[amount] = min_c
return cache[amount]
return dp(amount)
- 执行用时 :2192 ms, 在所有 Python 提交中击败了5.05%的用户
- 内存消耗 :46.9 MB, 在所有 Python 提交中击败了16.67%的用户